The Fair-Weather Atmosphere as a Power Source
Joseph M. Crowley
Electrostatic Applications
Abstract—The electric power available from the fair-weather field of the atmosphere is calculated by means of a Thevenin equivalent circuit. The maximum available power delivered to a load resistor directly connected to the ionosphere is on the order of tens of megawatts. For a collecting electrode at a lower elevation, the open-circuit voltage and short-circuit current are determined by the electric fields and current densities at that height, and also by the size of the collector. With current technology, the available power will be no larger than a few watts, and only a few applications seem worthwhile.
INTRODUCTION
Ever since Benjamin Franklin demonstrated electricity in the atmosphere and used it to ring a bell [1], people have attempted to extract usable amounts of energy from the air. Power generators have been patented [2] and electrostatic motors have been operated by atmospheric electricity [3], but practical problems such as the high impedance of the atmosphere, and the low energy density [4] compared to other sources have prevented any widespread use of this energy source.
As petroleum reserves dwindle, however, the need for alternate energy sources becomes more pressing. At the same time, many current and future devices require far less power than the traditional applications of heavy machinery, heating, transportation, and lighting. This has led to an exploration of several low-power sources for specialized applications [5], a search which has been given the name of “energy harvesting.”
Energy sources such as the kinetic motion of normal human activity, ambient lighting in offices, and RF fields have been demonstrated to supply enough power to operate some electronics devices. Although published work in using atmospheric power has been sparse, there have been numerous claims of success on the internet, and some seriously funded work has recently been contemplated.
In this paper, the energy that might be available from the atmosphere will be examined to determine the sorts of applications for which atmospheric electricity might be useful, and which are far-fetched. As a practical matter, only the fair-weather field will be considered, since it has several advantages over thunderstorms, including uniform distribution, constant availability, and absence of lightning.
THE GLOBAL ELECTRIC CIRCUIT
The earth, its atmosphere (including the ionosphere), and the local region of space influenced by the magnetic field of the earth are electrically active, with various mechanisms for the generation and transport of electricity. Although the electrical phenomena are distributed, it is often useful to approximate the major effects with a lumped-circuit model, called a global electric circuit [6–9].
These global circuit models vary in complexity, depending on how many effects are included. In general, the largest voltages, and also the highest resistances, occur between the earth and the ionosphere. Since this is the region where earth-based energy harvesting would take place, we will use a simplified model that includes only that region.
A typical lumped-element circuit for this region [7] is shown in Figure 1. The model is arranged vertically, with the earth at the bottom and the ionosphere at the top. Both the earth and the ionosphere are very good conductors compared to the atmosphere, so they can be considered as equipotentials. The values of the circuit elements shown in the figure are typical, but can vary with time of day, season, and location.
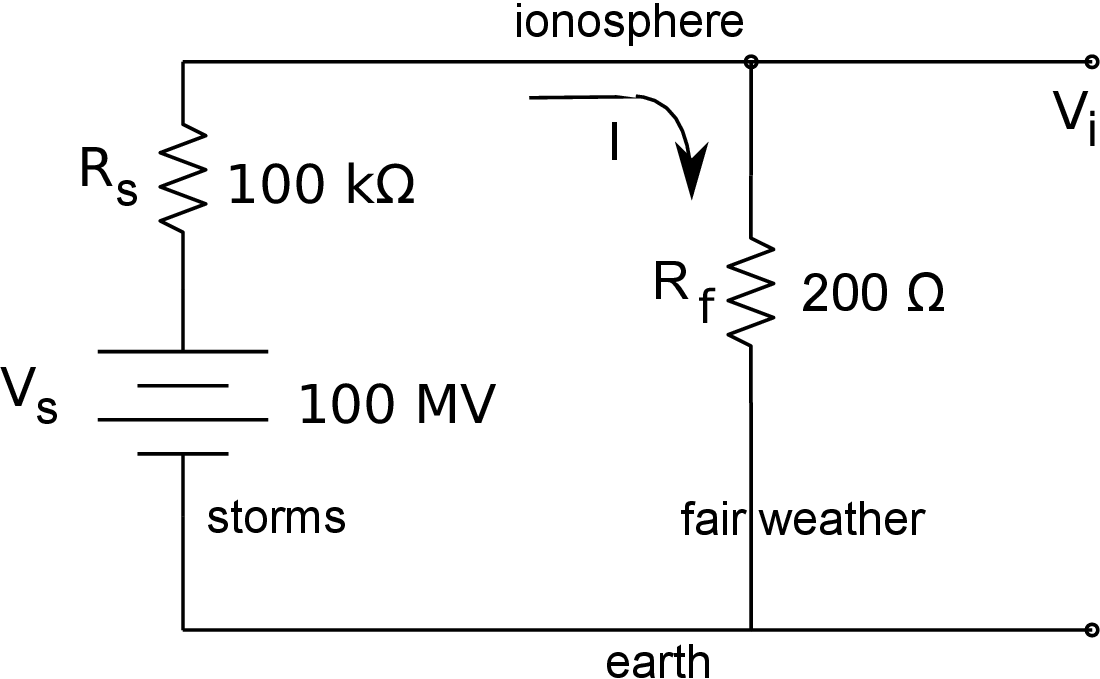
Fig. 1. The global electric circuit
The left branch represents all the thunderstorms on earth, which are the principal source of electricity in the atmosphere. Thunderstorms generate voltages by carrying positive charges upward on rising air currents. The charges are attached to relatively large particles of ice or water droplets. The large size of the particles generates enough drag that they cannot oppose the updraft, and are unable to return to recombine with the negative charges closer to the ground. This action is very similar to a van der Graaff generator, with the updraft replacing the belt. The voltage across the vertical extent of the storm reaches values on the order of \(V_{\mathrm{s}} \approx 100 \;\mathrm{M}\mathrm{V} \) .
As the voltage builds up, some of the charge is returned to ground as lightning or as an ionic flow, while the rest migrates up toward the ionosphere, which is at a lower potential than the top of the thunderstorm. The total resistance of the atmosphere above and below all the thunderstorms is represented by the storm resistance, with a typical value of \(R_{\mathrm{S}} \approx 100 \;\mathrm{k}\mathrm{Ω} \) . Since we have lumped all the thunderstorms into a single circuit branch, this resistance is really the parallel combination of all the atmospheric resistances above and below active storms. Once in the ionosphere, the charge is free to spread horizontally, since the horizontal resistance there is much less than an ohm [6].
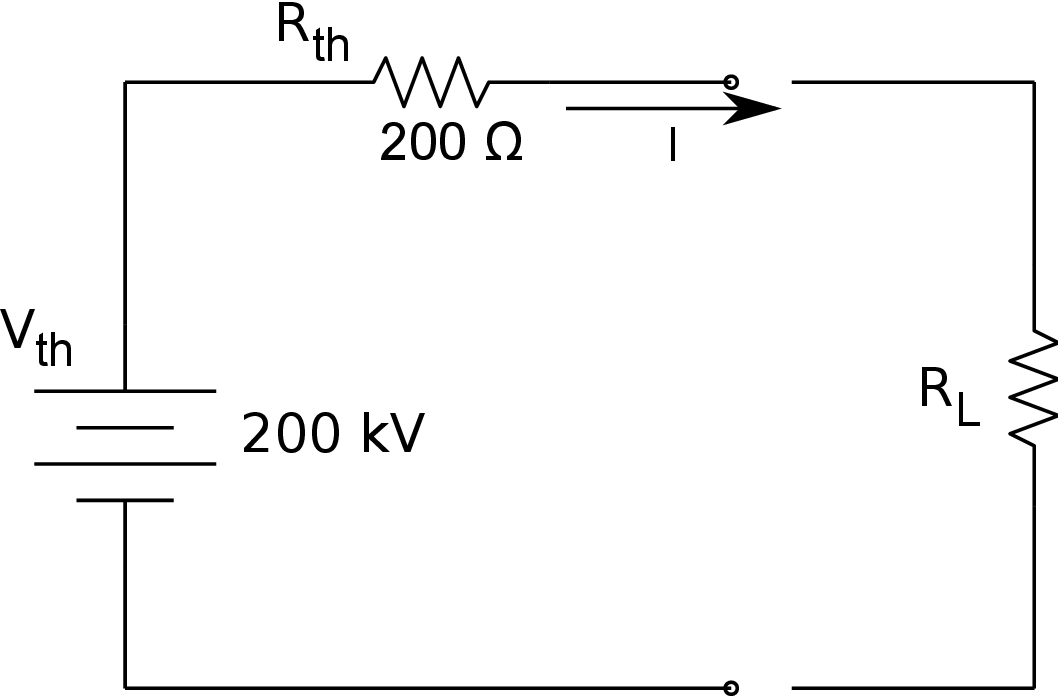
Fig. 2. Applying a load resistor from ionosphere to earth
Thunderstorms occur only over a small fraction of the earth. The rest of the atmosphere is electrically passive, with highly resistive air separating the conductive earth and ionosphere. The charge returns to earth through the passive, or fair-weather branch on the right of the circuit. The total fair-weather resistance of the atmosphere is approximately \(R_{\mathrm{f}} \approx 200 \;\mathrm{Ω} \) . It might seem surprising that the total resistance above thunderstorms is so much higher than in the fair-weather regions. This occurs because only a small fraction of the earth is covered with storms, while most is not. Thus there is a wide area for the fair-weather current flow, which makes the total resistance there much lower.
The storm and fair-weather resistances form a voltage divider. The open-circuit voltage between the ionosphere and the earth is given by
| (Eq. 1) | $$ \begin{aligned} \label{} V_{\mathrm{i}} = \frac{R_{\mathrm{f}}} { R_{\mathrm{s}} + R_{\mathrm{f}}} V_{\mathrm{s}} \approx \frac{R_{\mathrm{f}}} { R_{\mathrm{s}}} V_{\mathrm{s}} = \left(\frac{200}{100 \times 10^{3}}\right) (100 \times 10^{6}) = 200 \;\mathrm{k}\mathrm{V} \end{aligned} $$ |
The steady-state current in the global circuit is
| (Eq. 2) | $$ \begin{aligned} \label{} I = \frac{V_{\mathrm{s}}} {R_{\mathrm{s}} + R_{\mathrm{f}}} \approx \frac{V_{\mathrm{s}}} {R_{\mathrm{s}}} = \frac{100 \;\mathrm{M}\mathrm{V}} {100 \;\mathrm{k}\mathrm{Ω}} = 1000 \;\mathrm{A} \end{aligned} $$ |
The total power associated with the global electric circuit can also be estimated from the model. The current flows through the sum of the storm and fair-weather resistances, dissipating power given by
| (Eq. 3) | $$ \begin{aligned} \label{} P = (R_{\mathrm{s}} + R_{\mathrm{f}}) I^2 \approx (1 \times 10^{5})(1000)^2 = 100 \;\mathrm{G}\mathrm{W} \end{aligned} $$ |
Unfortunately, most of this power is dissipated in the flow of charge out from the storm itself. Harvesting this power would require collection electrodes at the top and bottom of each thunderstorm, which appears to pose insurmountable practical problems. Thus the best we could do to collect energy from the atmosphere would be to make contact with the ionosphere in the fair-weather region that covers most of the earth.

Fig. 2. Applying a load resistor from ionosphere to earth
The Thevenin equivalent circuit for a connection directly to the ionosphere is shown in Figure 2, where \(V_{\mathrm{th}} = V_{\mathrm{oc}} \approx 200 \;\mathrm{k}\mathrm{V} \) is the open-circuit voltage and \(R_{\mathrm{th}} \approx 200 \;\mathrm{Ω} \) is the equivalent resistance. The short-circuit current would be \(I_{\mathrm{sc}} = V_{\mathrm{th}}/R_{\mathrm{th}}= 1000 \;\mathrm{A} \) . The maximum available power is obtained when the load resistor matches the internal resistance of the source. At this point, the voltage would be reduced to half the open circuit value, and half the short-circuit current would flow through the load resistor. Thus the maximum power than could be extracted from the ionosphere is
| (Eq. 4) | $$ \begin{aligned} \label{} P = \frac{1}{4} V_{\mathrm{oc}} I_{\mathrm{sc}} = \frac{1}{4} (200,000) (1000) = 50 \;\mathrm{M}\mathrm{W} \end{aligned} $$ |
Since the average electric power plant produces hundreds to thousands of megawatts, we could, at most, expect to replace one very small power plant by extracting all the power from the ionosphere. Of course, it is not clear how we could connect a electrode to the ionosphere, and there might be environmental problems associated with such a scheme. In the next section, the possibility of extracting smaller, but still useful amounts of power from the atmosphere will be explored.
LOCAL HARVESTING
If the collector is at a lower altitude than the ionosphere, it can only collect part of the current that is coming down in a local region, and that current is limited by the high resistance of the air, relative to the ionosphere. Such a collector might still be useful for some applications, depending on how much power could be harvested. In this chapter, the power output for a collector at a lower height will be estimated.
The harvested current will depend on the local current density and on the effective cross- sectional area of the collector. The average current density is given approximately by
| (Eq. 5) | $$ \begin{aligned} \label{} J = \frac{I}{A} \approx \frac{1000}{5.1 \times 10^{14}} = 2 \;\mathrm{p}\mathrm{A}/\mathrm{m}^2 \end{aligned} $$ |
where \(A = 5.1 \times 10^{14} \;\mathrm{m}^2 \) is the total surface area of the earth. Since the local collecting area is a small fraction of the earths surface, it has little effect on the rest of the atmospheric circuit, which maintains the same overall voltage and resistance.
The atmosphere is not uniformly conductive. Instead, its conductivity usually increases with height. The primary mechanism that creates charge carriers in the atmosphere is cosmic radiation, most of which is absorbed in the ionosphere. Some will penetrate below to ionize the atmosphere, but the ionization becomes progressively weaker at lower elevations. In the very lowest layers of the atmosphere, the conductivity is somewhat increased, due to radioactivity in the soil and other local effects. This region will be neglected here, since power harvesting near the surface of the earth implies a large overhead resistance from the air.
Although the conductivity varies continuously with altitude, piecewise linear approximations are often used to characterize the overall electrical nature of the atmosphere. This involves dividing the atmosphere into layers with essentially uniform conductivity. One conventional piecewise linear approximation [7] to the conductivity variation (Figure 3) has three layers of increasingly higher conductivity with height.
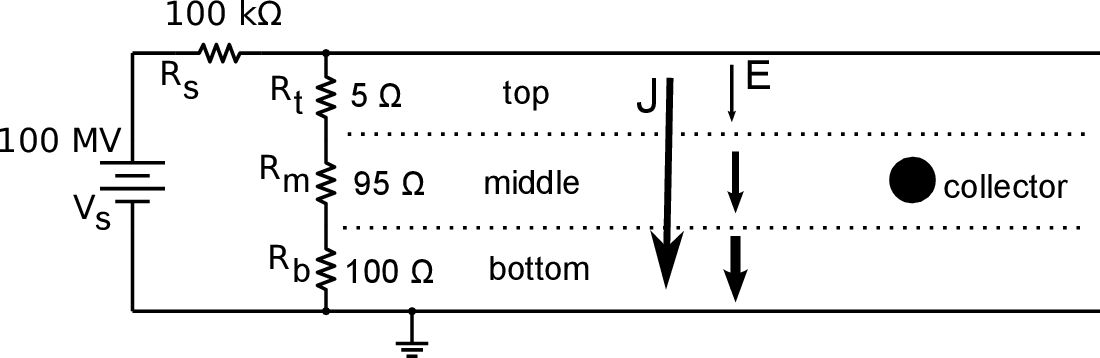
Fig. 3. Collecting electrode located between the ionosphere and the earth
The bottom layer represents the lowest 2 kilometers of the atmosphere, which has a relatively high resistance of \(R_{\mathrm{b}} = 100 \;\mathrm{Ω} \) . The middle layer extends from 2 to 10 kilometers, a distance of 8 kilometers. Although it is longer than the bottom layer, it has about the same resistance, since its conductivity is higher. The top layer extends from 10 kilometers to the base of the ionosphere, at 60 kilometers. Although this layer is thicker that the lower two layers, it has a very low total resistance due to its higher ionization.
Since the total current is the same regardless of altitude, the voltage drop across each of the three layers is given by
| (Eq. 6) | $$ \begin{aligned} \label{} V_{\mathrm{t}} &= R_{\mathrm{t}} I &= (5)(1000) &= 5 \;\mathrm{k}\mathrm{V}\\ V_{\mathrm{m}} &= R_{\mathrm{m}} I &= (95)(1000)& = 95 \;\mathrm{k}\mathrm{V}\\ V_{\mathrm{b}} &= R_{\mathrm{b}} I &= (100)(1000) &= 100 \;\mathrm{k}\mathrm{V}\\ \end{aligned} $$ |
The electric fields in the layers will depend on the thickness of the layer, in addition to the voltage drop. They are
| (Eq. 7) | $$ \begin{aligned} \label{} E_{\mathrm{t}} &= V_{\mathrm{t}} / h_{\mathrm{t}} &= 5 \;\mathrm{k}\mathrm{V}/50 \;\mathrm{k}\mathrm{m} &= 0.1 \;\mathrm{V}/\mathrm{m} \\ E_{\mathrm{m}} &= V_{\mathrm{m}} / h_{\mathrm{m}} &= 95 \;\mathrm{k}\mathrm{V}/8 \;\mathrm{k}\mathrm{m} &= 11.9 \;\mathrm{V}/\mathrm{m}\\ E_{\mathrm{b}} &= V_{\mathrm{b}} / h_{\mathrm{b}} &= 100 \;\mathrm{k}\mathrm{V}/2 \;\mathrm{k}\mathrm{m} &= 50 \;\mathrm{V}/\mathrm{m}\\ \end{aligned} $$ |
In the atmosphere, the potential increases from the ground in a non-linear fashion related to the electric field in each layer. The potential at any height, h, is given by
| (Eq. 8) | $$ \begin{aligned} \phi(h) = \left\{ \begin{array}{ll} V_{\mathrm{b}} + V_{\mathrm{m}} + E_{\mathrm{t}} \left(h - h_{\mathrm{b}} - h_{\mathrm{m}} \right) &\mbox{if $\;\; h_{\mathrm{b}} + h_{\mathrm{m}} \lt h \lt H$} \\ V_{\mathrm{b}} + E_{\mathrm{m}} \left( h - h_{\mathrm{b}} \right. &\mbox{if $\;\; h_{\mathrm{b}} \lt h \lt h_{\mathrm{b}}+h_{\mathrm{m}}$} \\ E_{\mathrm{b}} h &\mbox{if $\; \; 0\lt h \lt h_{\mathrm{b}}$} \\ \end{array} \right. \end{aligned} $$ |
A plot of this potential against height (Figure 4) for typical atmospheric conditions shows that the potential rises rapidly at first, and then levels off closer to the ionosphere. Even at the relatively low altitude of 2 km, the voltage is on the order of 100 kV, or about half the ionospheric voltage.
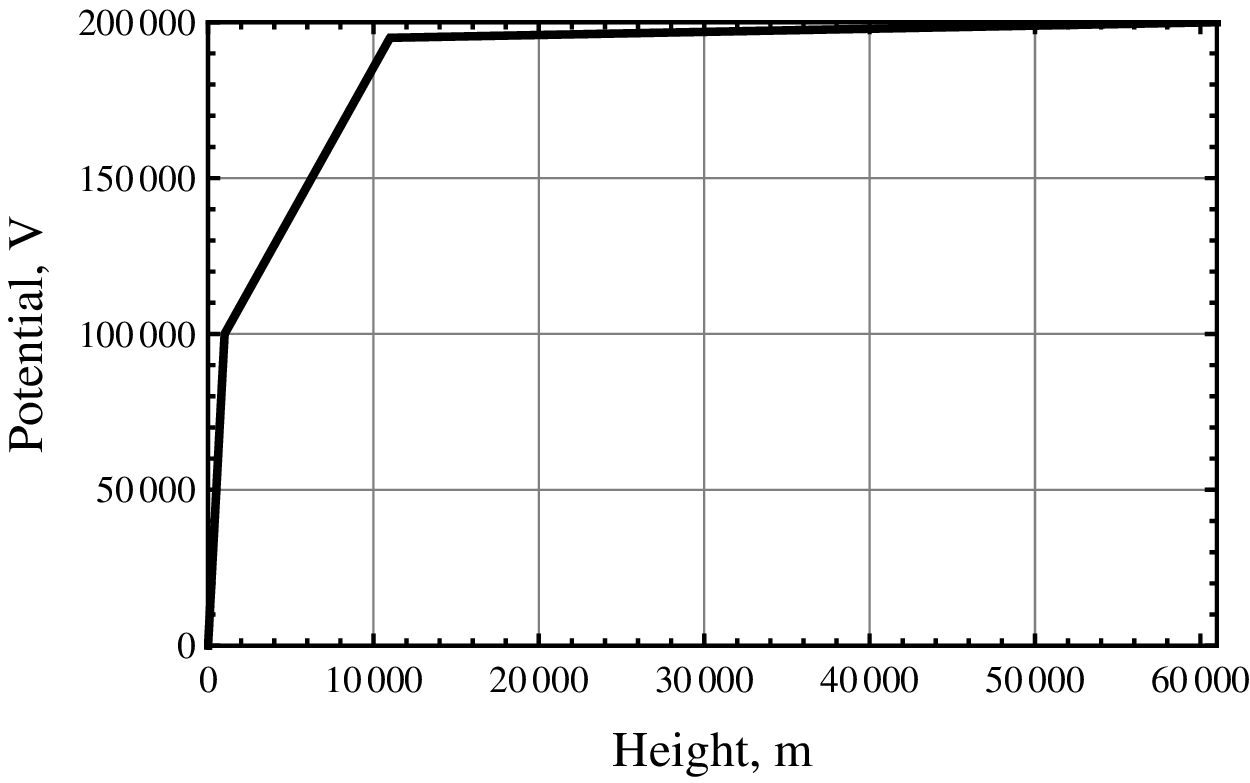
Fig. 4. Electric potential above ground
To collect power, we could insert a collecting electrode at some height in the atmosphere (as shown in Figures 3 and 5).
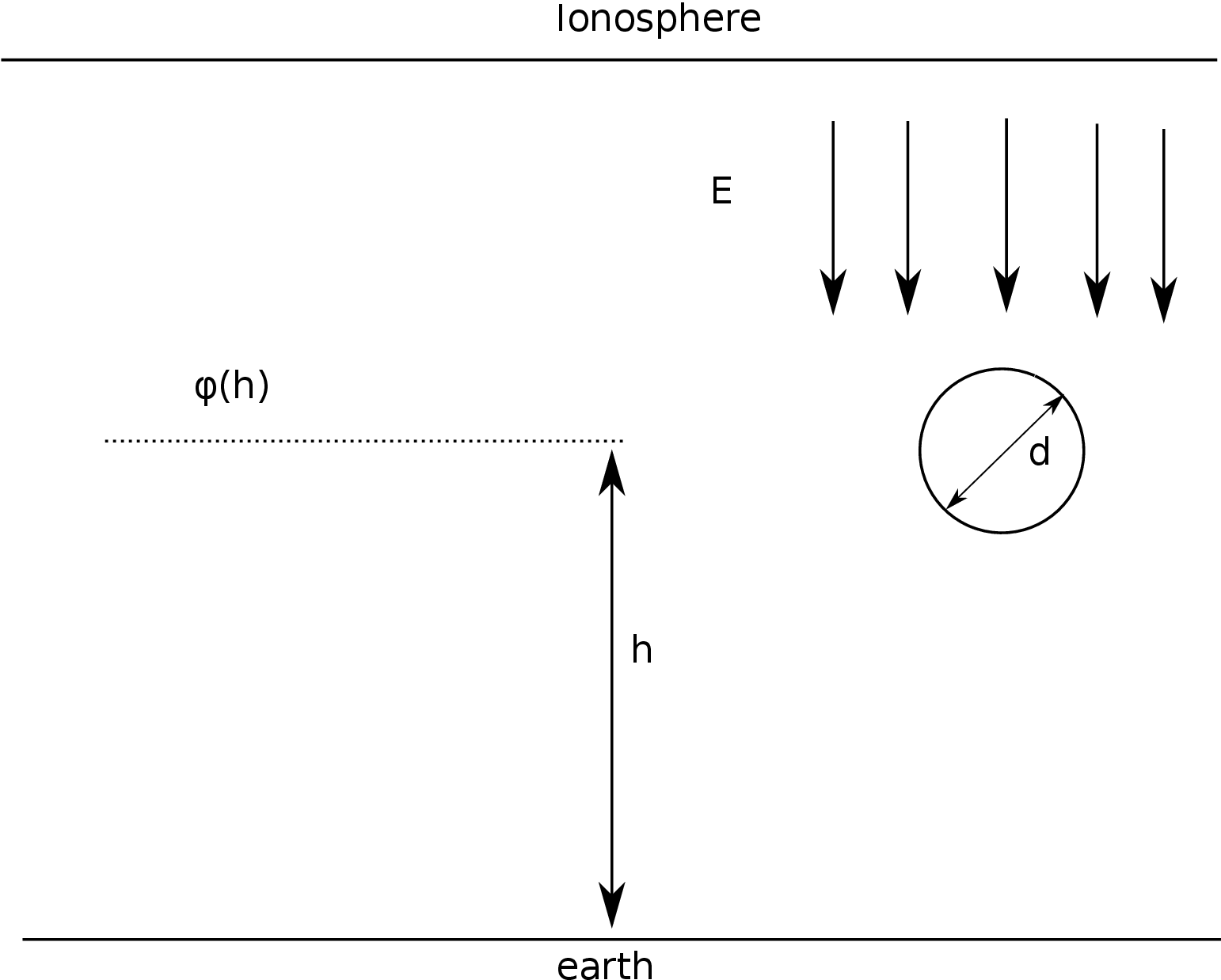
Fig. 5. Isolated collector in an electric field
The power collected from such an electrode will depend on the electric potential at its location, so placing the electrode higher will be to our advantage. The maximum power available from such a collector can be calculated from the open-circuit voltage and short-circuit current for the collector as
| (Eq. 9) | $$ P = \frac{ V_{\mathrm{oc}} I_{\mathrm{sc}} } { 4 } $$ |
Open circuit voltage
The open circuit voltage on the collector is the voltage that it would reach when suspended at a given height above ground. Although the collector could have any shape, we will assume that it is spherical, with a diameter d, in the interests of simplicity. We will also assume that the collector is elevated far above ground, at a height h that satisfies the relation
| (Eq. 10) | $$ \begin{aligned} h \gg d \end{aligned} $$ |
so that image charges can be neglected.
If the isolated collector were initially uncharged, it would distort the electric field in its vicinity. The electric potential in the vicinity of the sphere is given by [10]
| (Eq. 11) | $$ \begin{aligned} \label{} \phi = E_0 R \left[ r - \left(\frac{R}{r}\right)^2 \right] \cos \theta \end{aligned} $$ |
The radial and azimuthal components of the field are given by
| (Eq. 12) | $$ \begin{aligned} \label{e.efielddistort} E_r &= &-E_0 &\left[ 1 + 2 \left(\frac{R}{r} \right)^3 \right] \cos (\theta)\\ E_\theta &= &+E_0 &\left[ 1 - \left(\frac{R}{r} \right)^3 \right] \cos (\theta)\\ \end{aligned} $$ |
with the normal electric field at the surface of the collector given by
| (Eq. 13) | $$ \begin{aligned} \label{} E_r(r=R) = 3 E_0 \cos \theta \end{aligned} $$ |
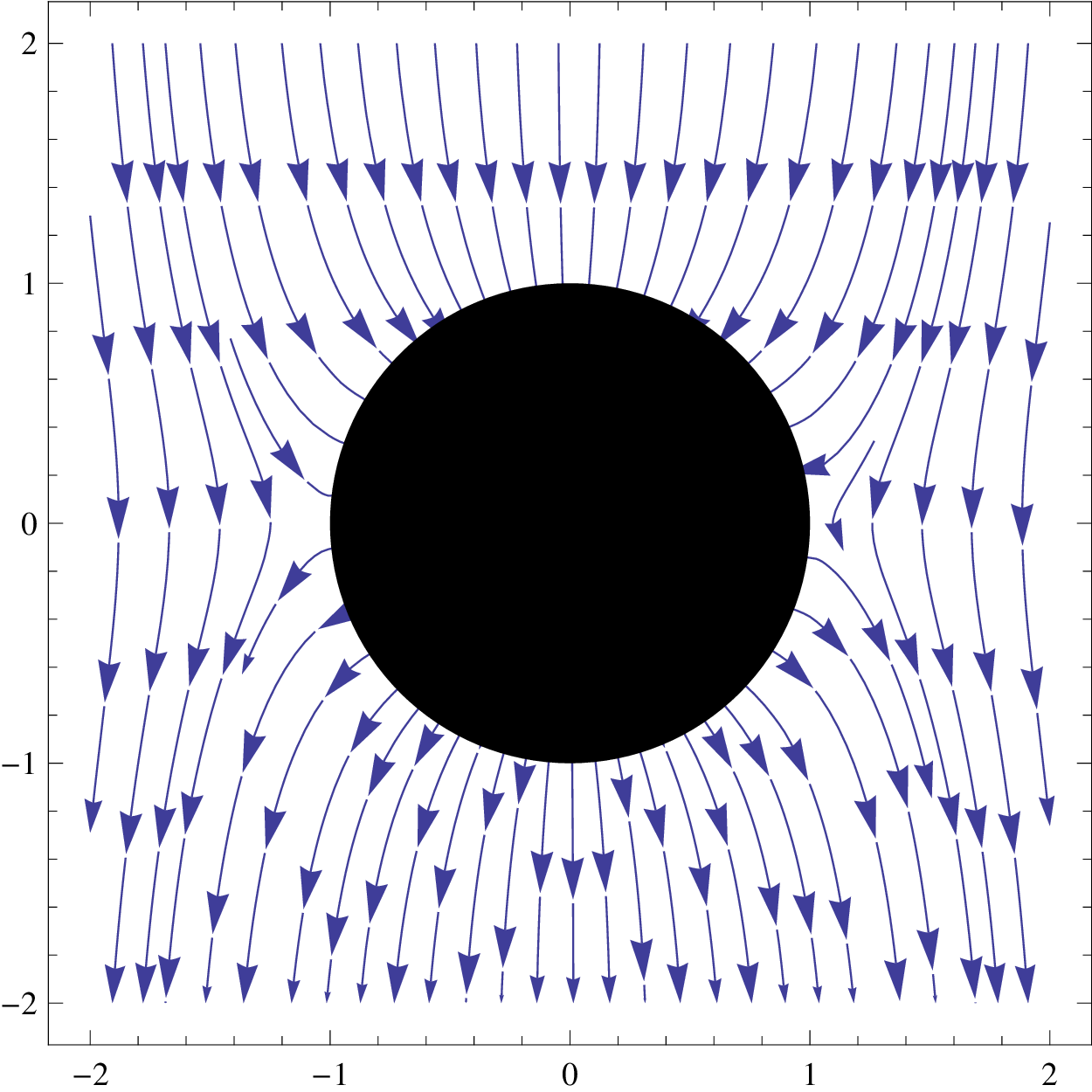
This is the situation shown in Figure 6(a) with the field lines going in at the top and out at the bottom.
|
|
| (a) At local potential | (b) After acquiring charge |
Fig. 6. Electric fields around an open-circuit collector
Any charged particles in the vicinity would follow these field lines toward the collector. Positive charges would arrive from above, and negative from below, at rates that depend on the density, mobility, and charge for each particle species. If the rates are identical, the charges will exactly recombine on the electrode, which will remain neutral overall. In this case, the voltage on the collector would be equal to the local potential of the atmosphere, as given by Equation 8.
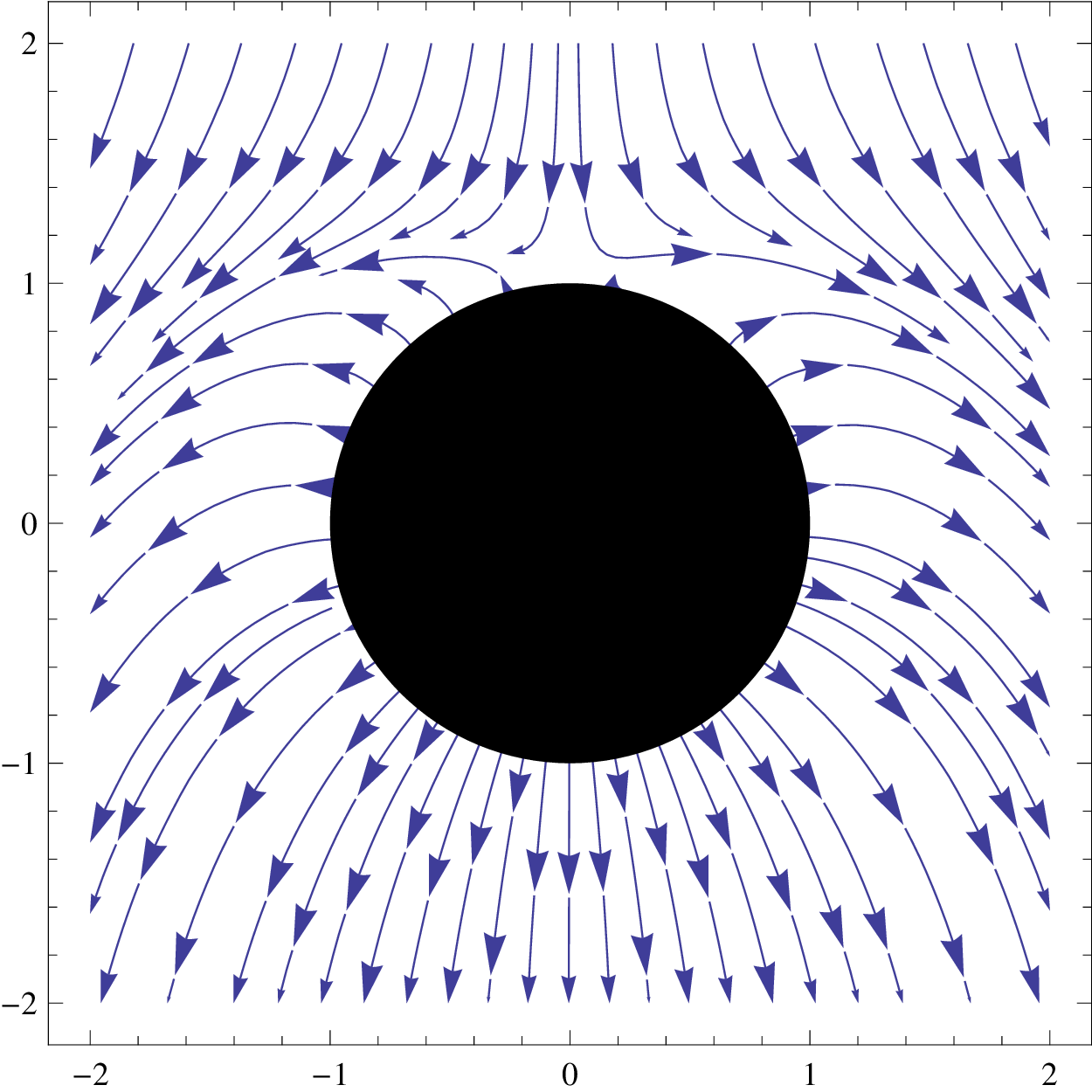
If the fluxes are not balanced, which is the normal situation, a net charge will build up on the electrode, which will alter its potential. The charge buildup continues until the electric field from the charge on the collector is large enough to overcome the imbalance in ion flux, leading to a situation similar to that shown in Figure 6(b).
The most extreme situation occurs when only a single polarity of ion is present. For example, if there are only positive ions present, they would be attracted most strongly to the top of the electrode, where the field is \(3 E_0 \) . Positive ions would continue to flow to this location until the charge on the collector became strong enough to repel them. The repelling field at the surface of the sphere is given by [10, p. 70]
| (Eq. 14) | $$ \begin{aligned} \label{} E = \frac{q}{4 \pi \epsilon R^2} \end{aligned} $$ |
This field becomes strong enough to stop further charging when
| (Eq. 15) | $$ \begin{aligned} \label{} 3E_0 = \frac{q}{4 \pi \epsilon R^2} \end{aligned} $$ |
so the collector will eventually build up a charge of
| (Eq. 16) | $$ \begin{aligned} \label{} q = 12 \pi \epsilon R^2 E_0 = 3 \pi \epsilon d^2 E_0 \end{aligned} $$ |
This is known as the Pauthenier charge limit.
A charged sphere will have a potential that differs from the local potential by an amount that depends on its capacitance, as given by
| (Eq. 17) | $$ \begin{aligned} \label{} V = \frac{Q}{C} \end{aligned} $$ |
Since the collector is far above the ground plane, its capacitance is just that of an isolated sphere, or
| (Eq. 18) | $$ \begin{aligned} \label{} C = 4 \pi \epsilon R = 2 \pi \epsilon d \end{aligned} $$ |
Thus the charge on the collector changes its voltage relative to local potential by
| (Eq. 19) | $$ \begin{aligned} \label{} V = \frac{Q}{C} = \frac{3 \pi \epsilon d^2 E_0} {2 \pi \epsilon d} = \frac{3}{2} E_0 d \end{aligned} $$ |
The open circuit voltage of the collector is therefore in the range
| (Eq. 20) | $$ \begin{aligned} \label{} \phi(h) - \frac{3}{2} E_0 d \lt V_{\mathrm{oc}} \lt \phi(h) + \frac{3}{2} E_0 d \end{aligned} $$ |
In practice, the difference in ion flux between positive and negative ions is not very large. Typically, the positive ion flux is about 25% higher than the negative flux [11], so we would expect this to raise the voltage on the open-circuit collector somewhat, but not up to the Pauthenier limit.
In any case, the increase in voltage due to the Pauthenier effect is likely to be relatively small, especially at higher elevations. For example, the extra voltage on a sphere with a diameter of 100 meters in the middle layer above 2 km would be
| (Eq. 21) | $$ V_\mathrm{pau} = \frac{3}{2} E_\mathrm{m} d = \frac{3}{2}(11.9) (100) = 1.8 \; \mathrm{kV} $$ |
Short circuit current
The short-circuit current from the collector can be calculated by placing the collector at ground potential, and finding the total current that would be collected. This calculation is simplified by setting the local potential \(\phi(h) \) as the reference zero. Then, using superposition, we can calculate the fields around the collector by adding the fields generated by the atmospheric electric field (with the collector at zero volts) to the fields generated by a negative \( \phi(h) \) on the collector in the absence of the atmospheric field.
The solution for the external field alone has been obtained above as Equation 12 in the course of finding the open-circuit voltage. This will be added to the field caused by grounding the collector, as described below.
If the potential of the sphere is brought down to that of the earth, it will be offset from local potential by an amount \(-\phi(h) \) . Since the ground plane is very far away, the potential around the sphere will have the form
| (Eq. 22) | $$ \begin{aligned} \label{} \phi = - \frac{\phi(h)}{r/R} \end{aligned} $$ |
which sets up an electric field
| (Eq. 23) | $$ \begin{aligned} \label{} E_r = - \frac{\mathrm{d} \phi}{\mathrm{d} r} = - \frac{\phi(h) R}{r^2} \end{aligned} $$ |
Adding the contributions of the atmospheric field and the grounded collector, the total field at surface of the collector is
| (Eq. 24) | $$ \begin{aligned} \label{} E_r = - 3 E_0 \cos \theta - \frac{\phi(h)}{R} \end{aligned} $$ |
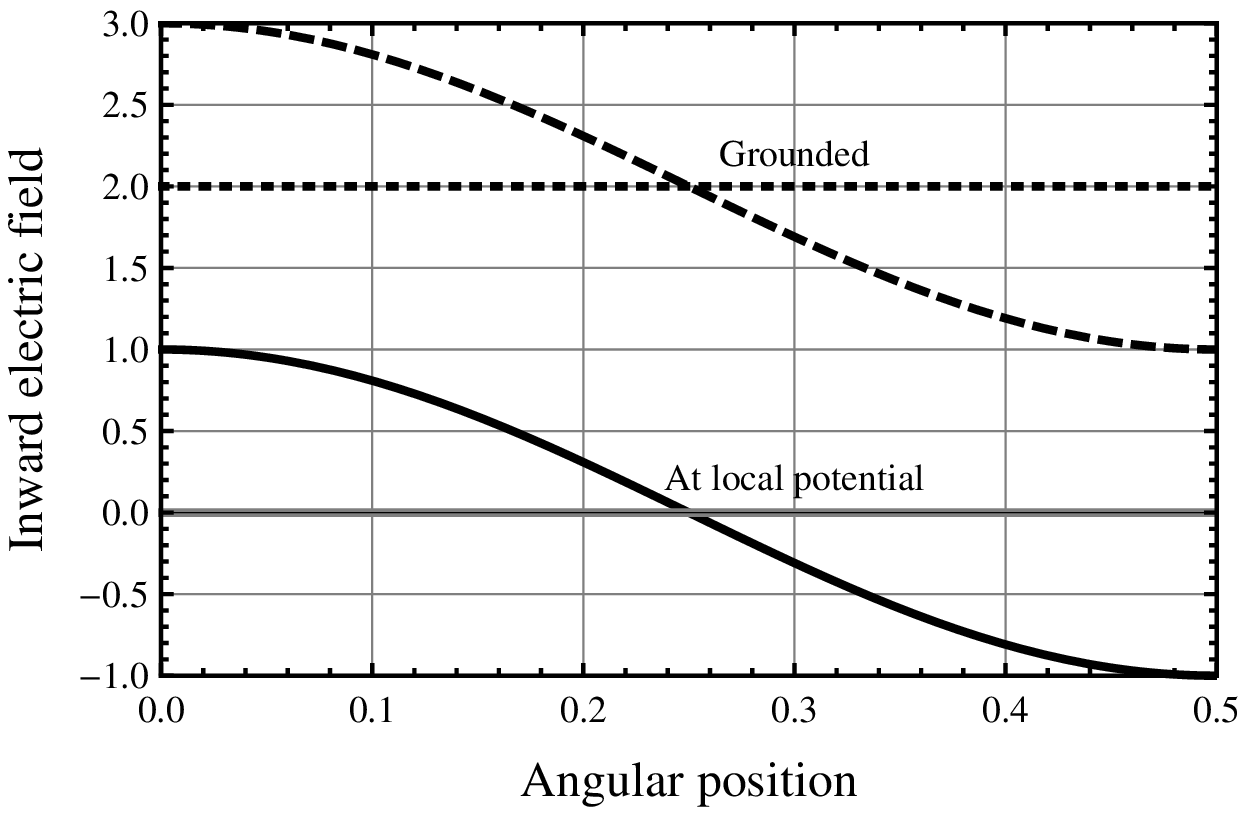
Fig. 7. Inward-directed field at the collector
A plot of inward-directed field (\(-E_r \)) at the surface of the collector is shown in Figure 7 as a function of angular position on the sphere. If the collector is located at \(h=0 \) , then there are equal areas of inward and outward fields, so that no net current would be collected, except for the Pauthenier effect described above. When the collector is elevated until
| (Eq. 25) | $$ \begin{aligned} \label{} \phi(h) \ge 3 E_0 R \end{aligned} $$ |
however, the field direction is inward all around the collector, with an average value given simply by the contribution of the voltage offset as
| (Eq. 26) | $$ \begin{aligned} \label{} E_r = - \frac{\phi(h)}{R} \end{aligned} $$ |
leading to an inward current of density of
| (Eq. 27) | $$ \begin{aligned} \label{} J_r = - \sigma E_r \end{aligned} $$ |
where \(\sigma \) is the electrical conductivity of the atmosphere.
If the collector is high enough to satisfy the condition of Equation 10, the short-circuit current to balloon would be the integral of the incoming current over the area of the collector
| (Eq. 28) | $$ \begin{aligned} \label{} I_{\mathrm{sc}} = \pi d^2 \sigma \frac{\phi(h)}{R} = \sigma \frac {\pi d^2 \phi(h)}{d/2} = 2 \pi d \sigma \phi(h) \end{aligned} $$ |
Note that for typical atmospheric conditions, the collector will always be negative relative to the local potential, which implies that positive ions are coming in to provide the current, or negative ions flow out from the collector. If the local atmosphere lacks positive ions, it would be necessary to provide negative ions, perhaps by corona points on the collector [2], or by radioactivity.
The current will depend on the local conductivity \(\sigma (h) \) of the atmosphere. Recalling that the downward current density
| (Eq. 29) | $$ \begin{aligned} \label{} J = \sigma(h) E_0(h) \end{aligned} $$ |
is independent of altitude, we can replace the conductivity with
| (Eq. 30) | $$ \begin{aligned} \label{} \sigma(h) = \frac{J}{E_0(h)} \end{aligned} $$ |
to write the short-circuit current as
| (Eq. 31) | $$ \begin{aligned} \label{e.isc} I_{\mathrm{sc}} = \frac{\phi(h)}{E_0(h) d} 2 \pi d^2 J = \frac{\phi(h)}{E_0(h)} 2 \pi d J \end{aligned} $$ |
The short-circuit current increases linearly with the diameter of the collector, so a larger collector will always increase the output.
Rewriting Equation 31 as
| (Eq. 32) | $$ \begin{aligned} \label{} I_{\mathrm{sc}} = \left(\frac{2\phi(h)}{E_0(h) d} \right) \pi d^2 J \end{aligned} $$ |
allows us to define a collection cross-section factor for the collector. Its physical cross sectional area is only \(\pi d^2 \) but it collects current from an area that is larger by the factor in parentheses. As an example, a 100-meter collector in the middle layer, with a local voltage slightly over 100 kV, and a local electric field of 11.9 V/m, would have an area enhancement factor of
| (Eq. 33) | $$ \begin{aligned} \label{} \frac{2\phi(h)}{E(h) d} =\frac{2 (100 \times 10^{3})}{(11.9) (100)} = 168 \end{aligned} $$ |
corresponding to collection over a diameter of about \(\sqrt{168}\; d = 1300 \;\mathrm{m} \) .
The increase in collection cross-section can be visualized by plotting the electric field lines (Equation 12) in the vicinity of the collector at different heights. Figure 8 shows these fields for a collector at two elevations.
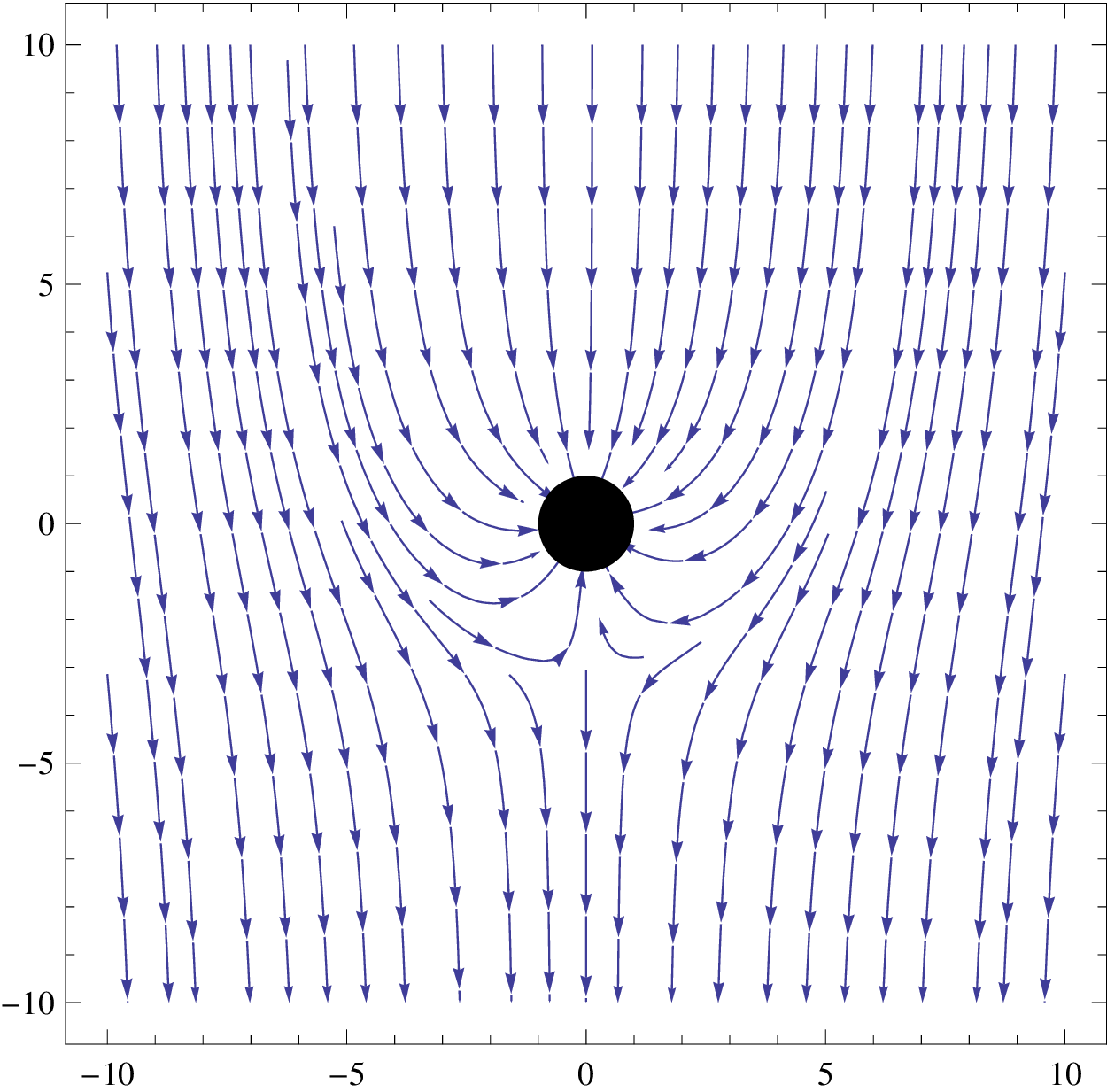
|
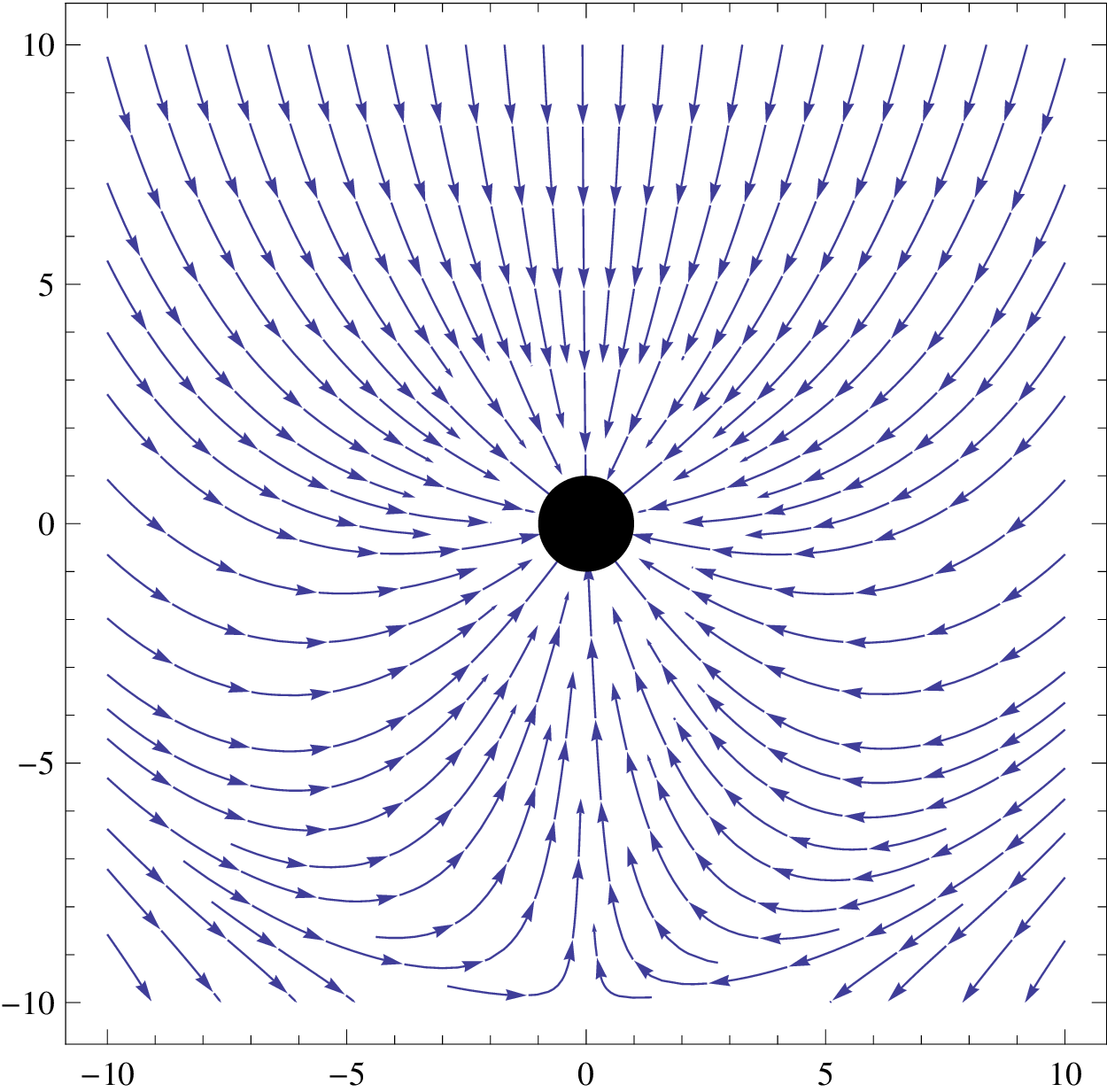
|
| (a) At low altitude | (b) At high altitude |
Fig. 8. Grounding the elevated collector attracts current from a wider area at higher elevations
It is clear that the collector at high elevations (on the right) is attracting ions from a much wider region, and will therefore have a much higher short-circuit current. If multiple collectors are deployed to increase the power output, they will be effective only if they are spaced far enough apart that they do not duplicate the collection area.
Available power
Now that the open-circuit and short-circuit behavior of the collector is determined, the equivalent circuit can be obtained. The voltage source is just the open circuit voltage of Equation 8 and the internal resistance is given by| (Eq. 34) | $$ \begin{aligned} \label{} R_{\mathrm{th}} = \frac{V_{\mathrm{oc}}} { I_{\mathrm{sc}}} = \frac{\phi(h)} { \frac{\phi(h)}{E_0(h) } 2 \pi d J } = \frac{E_0(h) } { 2 \pi d J } \end{aligned} $$ |
Since \(J = \sigma E_0 \) , the internal resistance can be written in terms of the local conductivity \(σ\) as
| (Eq. 35) | $$ \begin{aligned} \label{} R_{\mathrm{th}} = \frac{E_0(h) } { 2 \pi d \sigma E_0(h) } = \frac{1 } { 2 \pi d \sigma } \end{aligned} $$ |
A typical value for a 100-meter collector in the middle layer is
| (Eq. 36) | $$ \begin{aligned} \label{} R_{\mathrm{th}} = \frac{E_0(h) } { 2 \pi d J } = \frac{11.9 } { 2 \pi (100) (2 \times 10^{-12}) } = 9.5 \;\mathrm{G}\mathrm{Ω} \end{aligned} $$ |
The power available from the elevated collector is given in terms of the open-circuit voltage and the short-circuit current as
| (Eq. 37) | $$ \begin{aligned} \label{} P = \frac{1}{4} V_{\mathrm{oc}} I_{\mathrm{sc}} % = \frac{1}{4} % \frac{\phi(h)}{E_0(h)} 2 \pi d J % \phi(h) = \frac{\pi }{2} \frac{ J d \phi(h)^2 }{E_0(h)} = \left(\frac{ 2 \phi(h) }{E_0(h) d}\right) \frac{\pi d^2J \phi(h) }{4} \end{aligned} $$ |
The first factor is the area enhancement factor, while the second factor represents the power that could be obtained from an area equivalent to the physical cross-sectional area of the collector.
For a 100-m collector in the lower part of the middle layer, the power is on the order of
| (Eq. 38) | $$ \begin{aligned} \label{} P = \frac{\pi }{2} \frac{ (2 \times 10^{-12})(100) (100 \times 10^{3})^2 }{11.9} = 0.26 \;\mathrm{W} \end{aligned} $$ |

Fig. 9. Power collected as a function of height for diameters of 10, 100, and 1000 meters
Figure 9 shows the available power as a function of collector diameter for several altitudes. It is clear that more power is available at higher elevations. For a very large collector (1000 m) above 10 km, the power might approach a kilowatt. For smaller collectors, and lower altitudes, the available power will be much smaller, ranging from watts to microwatts.
DISCUSSION
The atmosphere can serve as a power source, but the power available is quite limited. The available power increases with the size of the collector, and with its elevation, so the usefulness of this power source has to be balanced against the cost of the collector and its support equipment, compared to more traditional sources.
The analysis presented above suggests that the maximum power to be expected by harvesting fair-weather atmospheric electricity is on the order of a kilowatt (or of a horsepower). It will never be feasible to power an automobile or a contemporary household with atmospheric electricity, even in future developments lead to implausibly large collectors at very high altitudes.

Fig. 9. Power collected as a function of height for diameters of 10, 100, and 1000 meters
With current technologies, the available power is even smaller. For example, tethered balloons are often suggested as the basis for a collector electrode. At present, large tethered balloons are available with a size on the order of 50 meters, and can operate at altitudes of about 5 kilometers [12]. From Figure 9, such a balloon might provide power on the order of watts. For local applications, a collector might be a smaller balloon (around 1 meter) on a shorter tether (perhaps 200 meters). Figure 9 predicts that this collector might furnish about 10 microwatts.
Another possibility is a ground-based structure, with the collector at the top. Towers and buildings over 500 meters tall exist today [13], and might conceivably be topped with a collector on the order of 50 meters. Figure 9 suggests that such a collector might provide power on the order of 10 milliwatts.
With power levels well below a watt, there are only a few applications where fair-weather electrostatics might prove useful as a power source. In this range, it competes with energy harvesting techniques such as converting human motion via piezoelectric transducers, or powering passive RFID devices with radio waves. It might also be considered for trickle charging of an apparatus that would draw power infrequently.
It seems unlikely that the cost of the collector would justify its use as a provider of power to a ground-based user. It might be more useful as a power source to some device on a balloon or elevated structure. As one possibility, an active RFID device on a balloon could respond to a reader at much greater distances than would be possible with a passive RFID.
REFERENCES
[1] B. Franklin, “Letter from Benjamin Franklin to Peter Collinson dated September 1753,” in The Papers of Benjamin Franklin (L. W. Labaree, ed.), vol. 5, p. 69, Yale University Press, 1962.
[2] H. Plauson, “Conversion of atmospheric electric energy.” US Patent 1,540,998, June 9, 1925.
[3] O. Jefimenko, “Operation of electric motors from atmospheric electric field,” Am. J. Phys., vol. 39, pp. 776–779, 1971.
[4] M. L. Breuer, “Feasibility of tapping atmospheric charge as a power source,” Renewable Energy, vol. 28, pp. 1121–1127, 2003.
[5] R. K. Cavin III and V. V. Zhirnov, eds., SRC/ATIC Forum on Minimum Energy Electronic Systems, (Abu Dhabi), May 23 and 24, 2010.
[6] R. G. Roble and I. Tzur, “The global atmospheric-electrical circuit,” in The Earth’s Electrical Environment, p. 206ff, National Academy Press, 1986.
[7] M. J. Rycroft, S. Israelsson, and C. Price, “The global atmospheric electric circuit, solar activity and climate change,” J. Atmos. Solar-Terrestrial Phys., vol. 62, pp. 1563–1576, 2000.
[8] M. J. Rycroft, “Electrical processes coupling the atmosphere and ionosphere: An overview,” J. Atmos. Solar-Terrestrial Phys., vol. 68, pp. 445–456, 2006.
[9] B. A. Tinsley, “The global atmospheric electric circuit and its effects on cloud microphysics,” Reports on Progress in Physics, vol. 71, p. 1ff, 2008.
[10] J. M. Crowley, Fundamentals of Applied Electrostatics, Laplacian Press, 1986.
[11] W. F. G. Swann, “Atmospheric electricity,” in International Critical Tables, pp. 442–445, McGraw-Hill, 1929.
[12] “Tcom 71m®- our premier aerostat.” Available: http://www.tcomlp.com/71M.htm. Retrieved May 6, 2011.
[13] “List of tallest buildings and structures in the world.” Available: http://en.wikipedia.org/wiki/List_of_tallest_buildings_and_structures_in_the_world. Retrieved May 6, 2011.
 Electrostatic Applications
Electrostatic Applications